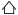
- 과학향기 Story
- 카드뉴스
카드뉴스
겹치지 않는 무한 패턴은 가능할까? 수학계 50년 난제, 비주기적 타일링 해결되다
2023년 07월 10일1
KISTI의 과학향기
겹치지 않는 무한 패턴은 가능할까?
수학계 50년 난제,
비주기적 타일링 해결되다
제공: David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, 2023
글 김청한 과학칼럼니스트
디자인 동아S&C
겹치지 않는 무한 패턴은 가능할까?
수학계 50년 난제,
비주기적 타일링 해결되다
제공: David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, 2023
글 김청한 과학칼럼니스트
디자인 동아S&C
2
욕실 타일, 보도블록, 벽지 같은 일상 속 무늬부터
경복궁, 알함브라 궁전 같은 전통 건축물까지
경복궁, 알함브라 궁전 같은 전통 건축물까지
우리는 수많은 반복 패턴을
어렵지 않게 접할 수 있다.
어렵지 않게 접할 수 있다.
3
그런데 이런 타일링이
수학계에선 50년도 넘은 어려운 문제다.
수학계에선 50년도 넘은 어려운 문제다.
일정한 모양이 반복되는 일반 타일링이 아닌,
비슷하면서도 다른 형태로 끝없이 평면을 채우는
비주기적 타일링(aperiodic tiling) 얘기다.
비슷하면서도 다른 형태로 끝없이 평면을 채우는
비주기적 타일링(aperiodic tiling) 얘기다.
4
비주기적 타일링을 얻기 위한
학자들의 노력은 1963년부터 가시화됐다.
학자들의 노력은 1963년부터 가시화됐다.
미국 수학자인 로버트 버거가
도형 2만 426개를 동원해 반복된 형태 없이
평면을 채울 수 있음을 증명한 것이다.
도형 2만 426개를 동원해 반복된 형태 없이
평면을 채울 수 있음을 증명한 것이다.
5
이후 많은 학자들이
비주기적 타일링 문제에 도전했다.
비주기적 타일링 문제에 도전했다.
그러다 1974년 수학자 겸 물리학자인
로저 펜로즈가 단 2개의 도형만으로
비주기적 타일링을 구현하는 데 성공했다.
로저 펜로즈가 단 2개의 도형만으로
비주기적 타일링을 구현하는 데 성공했다.
6
‘도형 하나로 비주기적 타일링 구현하기’는
대표적 수학 난제 중 하나로
많은 이들의 머리를 괴롭혔다.
대표적 수학 난제 중 하나로
많은 이들의 머리를 괴롭혔다.
그런데 최근 50여 년 만에
이에 대한 실마리가 풀렸다.
이에 대한 실마리가 풀렸다.
7
주인공은 바로,
영국 아마추어 수학자 데이비드 스미스와 그의 연구팀이다.
영국 아마추어 수학자 데이비드 스미스와 그의 연구팀이다.
연구팀은 13각형 도형을 바탕으로 패턴이 겹치지 않는
무한 평면 배치가 가능함을 증명해
학술지 네이처(Nature)에 발표했다.
무한 평면 배치가 가능함을 증명해
학술지 네이처(Nature)에 발표했다.
8
연구진은 도형의 이름을 아인슈타인이라 명명했는데,
과학자 ‘아인슈타인’과 ‘하나의 돌(ein+stein)’을
동시에 뜻하는 상징적 명칭이다.
과학자 ‘아인슈타인’과 ‘하나의 돌(ein+stein)’을
동시에 뜻하는 상징적 명칭이다.
아인슈타인은 지난 3월 연구진이 공개한
13각형 도형 ‘모자(hat)’를 조금 변형시킨 것이다.
13각형 도형 ‘모자(hat)’를 조금 변형시킨 것이다.
9
연구진은 출판 전 논문 공유 사이트 아카이브(arXiv)에서
모자를 통해 비주기적 타일링이 가능함을 증명한 바 있다.
모자를 통해 비주기적 타일링이 가능함을 증명한 바 있다.
모자를 여러 개 연결해 메타타일(metatile)을 만들고,
이를 모아 슈퍼타일(supertile)이 되는 과정을 반복하며
해당 작업이 무한히 계속될 수 있음을 보여준 것이다.
이를 모아 슈퍼타일(supertile)이 되는 과정을 반복하며
해당 작업이 무한히 계속될 수 있음을 보여준 것이다.
10
다만 지난 3월 발표에선 ‘모자’와 함께
‘좌우를 바꾼 모자’까지 총 2개 형태가 있어야
이러한 무한 형성이 가능했다.
‘좌우를 바꾼 모자’까지 총 2개 형태가 있어야
이러한 무한 형성이 가능했다.
이에 모자의 모양을 보완해
하나의 형태로도 비주기적 타일링을
구현한 것이다.
하나의 형태로도 비주기적 타일링을
구현한 것이다.
11
도형 하나로 구현 가능한 비주기적 타일링은
수학은 물론 공학에서도 중요도가 높다.
수학은 물론 공학에서도 중요도가 높다.
같은 구조 형태가 반복되는 것을 막아
소재의 내구성을 높이는 데 기여할 수 있기 때문이다.
소재의 내구성을 높이는 데 기여할 수 있기 때문이다.
비주기적 타일링과 특히나 연관 깊은
준결정(quasicrystal) 구조는
신소재공학의 중요한 연구 분야 중 하나다.
준결정(quasicrystal) 구조는
신소재공학의 중요한 연구 분야 중 하나다.
12
원자 배열이 규칙적인 결정과
그렇지 않은 비정질의 중간단계로서
마찰력이 적고 강도가 높아
코팅 소재를 만드는 데 유리하기 때문이다.
그렇지 않은 비정질의 중간단계로서
마찰력이 적고 강도가 높아
코팅 소재를 만드는 데 유리하기 때문이다.
준결정 구조는
골프채, 면도날, 프라이팬 같은 생활용품부터
엔진 단열재에 이르기까지 그 활용도가 높다.
골프채, 면도날, 프라이팬 같은 생활용품부터
엔진 단열재에 이르기까지 그 활용도가 높다.
13
풀리지 않았던 수학의 신비가 하나씩 밝혀지고
일상 속 소재와도 연관되는 것을 보면
수학이 이론에서 벗어나 현실에서도 무궁무진하게
활용될 수 있다는 것을
다시금 상기하게 된다.
일상 속 소재와도 연관되는 것을 보면
수학이 이론에서 벗어나 현실에서도 무궁무진하게
활용될 수 있다는 것을
다시금 상기하게 된다.

추천 콘텐츠
인기 카드뉴스
-
- 개복치, 정말 삐끗해도 죽을까? 돌연사 전문 개복치의 억울한 진실
- 개복치는 쟁반같이 넓적한 몸통에 뾰족한 지느러미가 위아래로 붙어있다. 이러한 못난 생김새 때문에 복어과를 뜻하는 ‘복치’에 대상을 낮출 때 쓰는 접두사 ‘개’가 붙어 개복치로 명명됐다. 라틴어로 맷돌을 뜻하는 학명 Mola mola도 이러한 개복치의 생김새에서 유래했다. 이러한 신기한 생김새를 가진 개복치는 일명 ‘돌연사’ 물고기로도 유명하다. 햇...
-
- 새콤달콤한 딸기는 과일이 아니다? 우리가 알던 식물 상식, 오해입니다만?!
- 겨울은 딸기의 계절이다. 딸기는 특유의 새콤달콤한 맛 덕분에 케이크, 잼, 주스, 빙수 등 디저트 재료로서 맹위를 떨치고 있다. 이런 딸기를 향한 대표적인 착각이 하나 있다. 바로 ‘딸기가 과일이라는 것’이다. 딸기는 과일이 아닌 ‘채소’로 분류된다. 여기서 과일과 채소의 차이가 무엇인지 알아보자. 사과, 배와 같은 과일은 나무에서 나는 여러해살...
-
- 스마트폰 중독이 인간관계에 끼치는 영향
- 같은 칼도 어떻게 쓰느냐에 따라 사람을 죽일 수도, 살릴 수도 있다. 결국 스마트폰과 인간관계도 마찬가지.무작정 부정적, 혹은 긍정적인 시각은 잠시 거두자. 이제 호모 모빌리쿠스 시대에 걸맞는 관계 맺기에 대해 고민이 필요한 때다.